Rounding with Python and Javascript

In the realm of data visualizations, the integrity and accuracy of displayed information are fundamental. As web developers, particularly those working in tandem with data scientists, one of our key responsibilities is to ensure that the data is represented accurately and consistently. This commitment to accuracy extends to every aspect of data handling, including something as seemingly trivial yet fundamentally important as rounding numbers.

Rounding numbers, both positive and negative, might appear to be a straightforward task at first glance. However, the method chosen for this process can significantly impact the interpretation and perception of data. Inaccurate or inconsistent rounding can lead to misleading visualizations, erroneous data interpretations, and ultimately, incorrect conclusions. Therefore, the choice of rounding method is not merely a technical decision but a critical aspect of data integrity and reliability.

In the world of data science, various rounding methods are employed, each with its own merits and use cases. Common methods include the traditional "round half up" (where .5 is always rounded up), "round half to even" (also known as bankers' rounding), and others. Each of these methods has implications for how data is aggregated and summarized.

For instance, the "round half to even" method is particularly useful in minimizing cumulative rounding errors in large datasets, thereby ensuring a more balanced and unbiased representation. This method rounds half numbers to the nearest even integer, which over a large set of data, distributes rounding upwards and downwards more evenly. It's especially pertinent in financial calculations, statistical data, and scenarios where equitable rounding is required.

As web developers, especially those involved in creating data visualizations, it is imperative that we align our rounding methods with those used by the data scientists. This alignment ensures consistency in how data is processed and presented, maintaining the integrity of the data from analysis to visualization. It also fosters a collaborative environment where data scientists and developers work in harmony, each respecting and understanding the methodologies and constraints of the other.

In conclusion, the choice of a rounding system is not merely a technicality but a cornerstone in the accurate and ethical presentation of data. As professionals responsible for presenting data in an understandable and truthful manner, we must be vigilant in our methods and mindful of their impact on data interpretation. By aligning our rounding methodologies with those of the data scientists, we uphold the standards of accuracy and integrity essential in data visualizations.

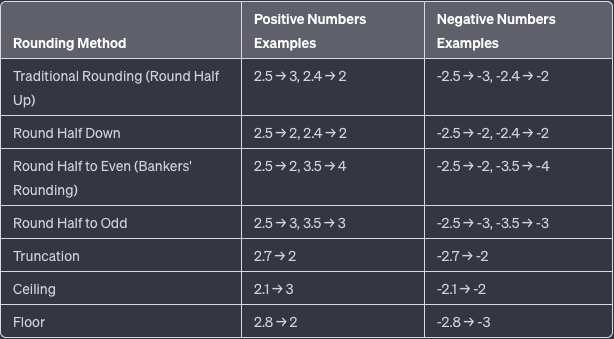
Below we present each of the available rounding methodologies, along with a clear example to understand how each of them work:

Python's Rounding Methods

Python, a language renowned for its versatility and efficiency in data science and web development, offers various methods for rounding numbers. However, it's crucial to understand that not all native Python methods are universally applicable or align with specific rounding methodologies that may be required in certain scenarios. This often necessitates the creation and use of custom functions to meet precise rounding standards.

Python's native round() function adheres to the "Round Half to Even" method, commonly known as bankers' rounding. While this is suitable for many applications, especially in financial calculations, there are instances where different rounding methodologies are more appropriate. For instance, in statistical analyses, scientific computations, or specific business logic, alternative rounding methods like "Round Half Up," "Round Half Down," "Round Half to Odd," and others may be more relevant.

Why do we use custom functions? for the following reasons:

Methodological Alignment: Data integrity and consistency are paramount. Aligning the rounding technique with the specific needs of a project or the methodologies used by data scientists is essential. Native Python functions may not always offer the flexibility or precision required for these specialized tasks.
Handling Negative Numbers: Python's round() function, while effective, behaves differently with negative numbers, rounding them towards zero. This can be problematic in datasets where negative values hold significant meaning, and consistent rounding logic is required regardless of the sign.
Specialized Rounding Rules: Certain projects may demand unique rounding rules that aren't catered to by Python's standard library. For instance, rounding towards the nearest odd number or implementing a "Round Half Down" approach requires logic beyond what is natively available.
Maintaining Data Fidelity: In data visualization and analysis, even minor discrepancies in rounding can lead to misinterpretations. Custom functions allow for precise control over the rounding process, ensuring that the data presented is as accurate and truthful as possible.

The upcoming section delves into various rounding methodologies, highlighting the limitations of Python's native functions and presenting custom solutions where necessary. From traditional rounding (Round Half Up) to more specialized methods like Round Half to Odd, each method is examined with examples to illustrate their implementation. Understanding these nuances and having the capability to implement custom rounding functions is a critical skill for web developers and data scientists alike, ensuring that the data is not just accurately processed, but also meaningfully represented.

Traditional Rounding (Round Half Up):

round(number) in Python doesn't support this natively for negative numbers. For positive numbers, it behaves normally, but for negative numbers, it rounds towards zero. Thus, a custom code is needed to be able to apply this rounding method. Here is an example:

import math

def round_half_up(n):
abs_n = abs(n)
sign = math.copysign(1, n)
return sign * math.floor(abs_n + 0.5)

Round Half Down:

You can achieve this rounding method with custom code, like the one below:

import math

def round_half_down(n):
    abs_n = abs(n)
    sign = math.copysign(1, n)
    if abs_n - math.floor(abs_n) == 0.5:
        return sign * math.floor(abs_n)
    return round(n)

Round Half to Even (Bankers' Rounding):

You can use the native round() function, which follows the bankers' rounding method:

number = 2.5
rounded_number = round(number)  # Will round to the nearest even number

Round Half to Odd:

No native function, so math comes back to the rescue:

import math

def round_half_to_odd(n):
    rounded = round(n)
    return rounded if rounded % 2 != 0 else rounded + (1 if n > 0 else -1)

Truncation:

Python's math.trunc() follows this method

import math

number = 2.7
truncated_number = math.trunc(number)  # Results in 2

Ceiling and Floor:

Use math.ceil() and math.floor().

import math

# Ceiling
number = 2.1
ceiling_number = math.ceil(number)  # Results in 3

# Floor
number = 2.8
floor_number = math.floor(number)  # Results in 2

JavaScript's Rounding Methods

In the dynamic landscape of web development, JavaScript stands as a pivotal language, especially in the domain of client-side scripting and interactive web applications. A crucial aspect of JavaScript programming, particularly when dealing with data visualization and processing, is the accurate and methodical rounding of numbers. JavaScript provides a suite of native methods for rounding, but understanding their nuances and limitations is key to ensuring data integrity and precision.

Why the need for custom functions in JavaScript ? Unlike Python, JavaScript's native rounding methods exhibit distinct behaviors, especially when dealing with negative numbers. This can pose challenges in scenarios where consistency and accuracy in rounding are non-negotiable, such as in financial calculations, statistical data analysis, and real-time data visualizations.

Consistency Across Data Types: JavaScript’s native methods, like Math.round(), behave differently for positive and negative numbers. For instance, Math.round() applies traditional rounding to positive numbers but not to negative numbers. This inconsistency can lead to skewed data representation, particularly in datasets where negative values play a crucial role.
Methodological Alignment: Aligning the rounding methodology with specific project requirements or with methodologies used in other programming environments (like Python) is essential. JavaScript's native methods might not always align with these requirements, making custom functions indispensable.
Specialized Rounding Methods: Certain projects may demand unique rounding approaches, such as "Round Half to Even" (Bankers' Rounding) or "Round Half to Odd". JavaScript does not provide native functions for these methods, necessitating the creation of custom functions to fill this gap.
Precision in Data Visualization: In web development, where JavaScript often drives the front-end data presentation, precision in rounding can have a significant impact on how users interpret data. Custom rounding functions allow developers to maintain control over how data is rounded and displayed, ensuring a truthful and accurate representation of the underlying data.

The following section explores JavaScript's native rounding methods and illustrates how to implement various rounding methodologies using JavaScript. From traditional rounding (Round Half Up) to more specialized methods like Round Half to Odd, each method is analyzed with examples to guide their implementation. This exploration is not just a technical endeavor but a commitment to maintaining the highest standards of data integrity and accuracy in the world of web development.

Traditional Rounding (Round Half Up)

The math.round() method follows the Traditional Rounding for positive numbers, but not for negative numbers, as you can see below.

Math.round(2.5); // 3
Math.round(-2.5); // -2

In order to really make sure it follows the traditional rounding, you need a custom function:

function roundHalfUp(n) {
  return n >= 0 ? Math.floor(n + 0.5) : Math.ceil(n - 0.5);
}

Round Half Down

function roundHalfDown(n) {
  return n > 0 ? Math.ceil(n - 0.5) : Math.floor(n + 0.5);
}

Round Half to Even (Bankers' Rounding)

JavaScript doesn't have a native method, so a custom function is needed. Here is a possible solution:

function roundHalfToEven(number) {
  // First, round the number to the nearest integer
  const rounded = Math.round(number);

  // Check if the number was a half (e.g., x.5)
  if (Math.abs(number - rounded) === 0.5) {
    // If the rounded number is odd, subtract 1 to make it even
    return rounded % 2 === 1 ? rounded - 1 : rounded;
  }

  // For non-half numbers, return the rounded value
  return rounded;
}

Round Half to Odd

No javascript method available, I'm afraid, but you can rely on a custom function:

function roundHalfToOdd(n) {
  let rounded = Math.round(n);
  return rounded % 2 === 0 ? rounded + 1 : rounded;
}

Truncation:

Math.trunc() removes decimal, which behaves like truncation.

Math.trunc(-2.7); // -2 4. Aligning JavaScript with Python

Ceiling and Floor

Math.floor() and Math.ceil() do the trick and ensure consistent behavior for positive and negative numbers.

Math.floor(-2.5); // -3
Math.ceil(2.3); // 3

Conclusion:

As we navigate the complexities of data representation in web development and data science, the importance of precise and consistent rounding techniques cannot be overstated. Our exploration of various rounding methods in Python and JavaScript underscores a fundamental truth: the methodology employed can significantly impact the accuracy and interpretation of data. This is especially critical in fields like finance, statistics, and data visualization, where even minor discrepancies can lead to substantial implications.

To facilitate a clearer understanding and to aid in the selection of appropriate rounding methods, we present a comprehensive table summarizing each rounding technique along with the corresponding functions in Python and JavaScript. This table serves as a quick reference guide, ensuring that developers and data scientists can make informed decisions that align with their project's specific requirements and methodologies.

In our journey through the nuances of rounding, we have seen that while native functions in Python and JavaScript provide a solid foundation, they often require augmentation through custom functions to meet specific rounding needs. This is particularly true when dealing with negative numbers, where native functions may not behave as intuitively expected, or when applying specialized rounding methods like Round Half to Odd.

The development of custom functions is not just a technical exercise but a commitment to maintaining the integrity and fidelity of data. It reflects an understanding that in the world of data science and web development, details matter—especially when these details pertain to how data is rounded and presented.

By equipping ourselves with a thorough understanding of these rounding methods and the tools available in Python and JavaScript, we empower ourselves to make informed decisions. This ensures that our data visualizations and analyses are not only accurate but also truthful, thus maintaining the trust and confidence of those who rely on our work.

In closing, remember that the choice of a rounding system is more than a mere technicality; it is a cornerstone in the ethical and accurate presentation of data. By aligning our methodologies and embracing the right tools, we uphold the highest standards of precision and integrity in our professional endeavors.